
Parte seconda
Nella prima parte, s’è detto qualcosa sulla vita e sul pensiero di una delle figure più affascinanti e misteriose della storia, sottolineando inoltre la circostanza rimarchevole che, nello stesso ristretto periodo temporale, il 6º secolo AEV, sui 4 assi più importanti del mondo, abbiano calcato contemporaneamente il palcoscenico le 4 guide spirituali più influenti dell’umanità:
Budda (Buddha), Confucio (Kǒng Fūzǐ), Lao-tze (Lǎozǐ) e Pitagora (Πυϑαγόρας).
Non c’è che dire: un risveglio del pensiero senza precedenti, una coincidenza straordinaria!
L’autore però aveva avvertito i suoi «25 lettori»[1] (leggi prima parte) di essere insensibile ad ogni soffio spirituale e immune dal fascino di qualsiasi Gurū. Quel che rende unico Pitagora ai suoi occhi è ben altro.
Pitagora fu il primo a definirsi filosofo (ϕιλόσοϕος), amante della sapienza, e fu il primo matematico ad essere noto con il proprio nome.
La definizione stessa di matematica (μάθημα), apprendimento, scienza, è un lascito del suo insegnamento.
La sua scuola era infatti divisa in 2 livelli:
- gli acusmatici (ἀκoυσματικός), coloro che ascoltano, cioè quelli che erano attratti dal misticismo ed i rituali;
- i matematici (μαθηματικός), coloro che apprendono, cioè quelli interessati ai numeri, ai loro rapporti e ad una conoscenza più approfondita. [2]
E solo ai matematici era concesso di parlare, fare domande e ricerche, gli altri potevano solo ascoltare.
E’ giunto ora il momento di provare a penetrare in quel livello di maggior approfondimento, e proprio a partire dal famoso teorema che da lui prende il nome, chiarendo innanzitutto che, quello speciale rapporto tra i lati del triangolo rettangolo, era già stato scoperto in Mesopotamia ed in Egitto almeno 1.000 anni prima della nascita di Pitagora.
Un reperto rinvenuto dall’archeologo Banks nell’area archeologica di Senkereh, un sito nel sud dell’attuale Iraq, risalente al 1800 AEV, il periodo della dinastia di Hammurabi, finito in seguito nella Plimpton Collection ed ivi catalogato con il numero 322, apparentemente è un’insignificante terracotta, una tavoletta di argilla di dimensioni modeste (13*9*2 centimetri).

Si tratta invece della straordinaria prova che i Babilonesi già conoscessero la trigonometria e quindi almeno alcuni casi particolari del celebre teorema.[3]
E’ risaputo pure che gli straordinari artefici delle piramidi, per verificare la perpendicolarità delle loro costruzioni, usassero l’espediente di tendere una corda con i nodi posti alla distanza di semplici intervalli regolari (3, 4 e 5), cioè la più piccola terna pitagorica primitiva, come si vedrà più avanti.
E’ suggestivo che architetto (ἀρχιτέκτων), il capo costruttore, fosse stato agli albori un tenditore di corde.
Ma se è così, perché attribuirlo a Pitagora? Qual è stato allora il suo contributo originale?
Sebbene gli antecedenti/predecessori del famoso teorema fossero già conosciuti presso le più importanti civiltà orientali dell’antichità, in Babilonia, Cina, Egitto e India, e molti storici diano per certo che fu proprio in quei luoghi che Pitagora ne venne per la prima volta a conoscenza, in occasione di uno dei suoi molteplici viaggi, non si può negare al matematico greco la sua parte di genialità, avendo trovato per primo una giustificazione rigorosa e generale del teorema omonimo, non empirica né limitata a pochi casi.
Ciò spinse Pitagora e i suoi allievi a ordinare la geometria in catene di deduzioni che, partendo da verità semplici ed evidenti, condussero gradualmente alla scoperta di proprietà sempre più riposte.
A Pitagora e ai primi pitagorici deve essere quindi attribuita la fondazione della geometria razionale.
Teorema di Pitagora, uno dei primi teoremi della geometria classica, di cui si riporta di seguito l’enunciato:
«il quadrato costruito sull’ipotenusa di un triangolo rettangolo è equivalente alla somma dei quadrati costruiti sui cateti».
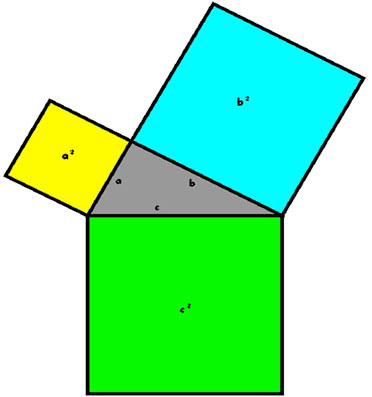
Una semplice proposizione, che in formula equivale a:
a2 + b2 = c2
In questo breve enunciato di Pitagora è racchiuso l’enorme salto dallo specifico al generale.
Non una lista di casi dei particolari triangoli rettangoli per i quali vale una certa proprietà ma un vero e proprio teorema (ϑεώρεμα), «esame, osservazione», uno schema teorico generale valido sempre per qualsiasi triangolo rettangolo, a prescindere dalle misure specifiche dei cateti (κάθετος), i lati tra di loro perpendicolari, cioè separati da un angolo retto (90°), e dell’ipotenusa (ὑποτείνουσα), la linea sottesa, quella che sostiene la costruzione.
A cosa serve tutto ciò? Immaginate un antico architetto alle prese con il problema di verificare se due pareti siano perpendicolari oppure no, tenendo in considerazione la difficoltà della misurazione degli angoli.
Ora non gli sarà più difficoltoso misurare gli angoli, gli basterà utilizzare una squadra con cateti e ipotenusa di misura rispettivamente uguale ad a, b e c, tali che a2 + b2 = c2 per essere sempre certo che quei cateti siano tra loro perfettamente perpendicolari e che quel triangolo sia proprio un triangolo rettangolo.
Tutte le terne di numeri che godono della suddetta relazione, da allora in poi, sono note con il nome di terne pitagoriche.
E tra loro, 3, 4 e 5, è la più piccola, come è immediato verificare: 32 + 42 = 52 = 9 + 16 = 25.
Da qui deriva il quartabuono, squadra del disegno tecnico, strumento per verificare la perpendicolarità ed in seguito deriveranno tante altre conquiste, come le successive generalizzazioni del teorema agli spazi n-dimensionali ed il concetto di distanza negli spazi euclidei o pseudoeuclidei, segno evidente di una utilità e vitalità ben lungi da esaurirsi nel presente.
Del teorema esistono molte dimostrazioni diverse, belle ed interessanti, vuoi per l’eleganza dell’approccio o dell’impostazione, vuoi per la curiosità o celebrità degli autori.
A partire da quella classica, contenuta già negli Elementi di Geometria di Euclide (Στοιχεῖα) ed insegnata ancora oggi su scala planetaria, passando per quella di Leonardo da Vinci, fino a quella di Lewis Carroll o di un presidente degli Stati Uniti.[4]
Il professor Elisha Scott Loomis nel 1927 raccolse e classificò ben 371 dimostrazioni diverse del teorema.[5]
Probabilmente quella originaria di Pitagora, disegnata sulla sabbia, si basava sul seguente schema:
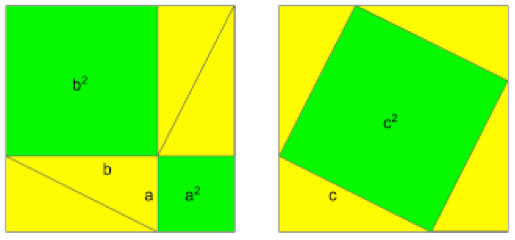
Diogene Laerzio riporta la notizia dell’enorme enfasi, che fece seguito alla sua dimostrazione, tanto da celebrarla addirittura con una ecatombe (ἑκατόμβη)[6] ma la notizia è palesemente in contraddizione con il conclamato vegetarianesimo di Pitagora e con il suo rispetto degli animali, anche a causa della sua dottrina della metempsicosi.
Pare certo che Pitagora avesse scoperto ed insegnato anche un metodo per ottenere le terne pitagoriche.
Secondo Proclo,[7] nell’Accademia di Platone (427–347 AEV) veniva insegnato il seguente metodo, attribuito alle leggendarie ricerche di Pitagora, che oggi sarebbe scritto con le seguenti formule:
a = 2μ
b = μ 2 − 1
c = μ 2 + 1
Attribuendo a μ valori diversi in numeri interi, si ottengono agevolemente le prime terne:
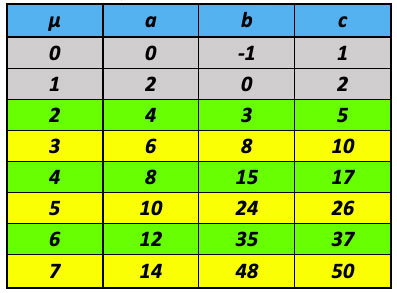
Si vede subito che, per μ = 0, μ = 1, le terne sono degeneri (0,−1, 1; 2, 0, 2) e non vi è alcun triangolo; oltre tutto, per i Greci 0 e 1 non erano veri e propri «numeri», -1 men che meno, così quei valori sono da scartare.
Per μ = 2, il triangolo rettangolo è ben formato e le misure dei suoi lati (a = 4; b = 3; c = 5) formano la più piccola terna pitagorica primitiva, come già detto.
Similmente sono evidenziate in verde le altre terne primitive, mentre in giallo sono evidenziate le terne derivate.
Una terna è primitiva se e solo se sono primi tra loro gli interi che la compongono, negli altri casi è derivata.
E’ agevole osservare che, per μ dispari si ottengono terne pitagoriche derivate, costituite da tre numeri pari. Ad esempio, per μ = 7, la terna (14, 48, 50) è derivata dalla primitiva (7, 24, 25), che invece è assente da quel primo elenco dato che, per μ pari, si ottengono alcune terne pitagoriche primitive ma non tutte.
Per la soluzione completa, al problema di trovare tutte le terne primitive, occorrerà attendere Diofanto di Alessandria (250-350 EV) e la sua Aritmetica (ἀριϑμητική), «scienza dei numeri» di chiara ispirazione pitagorica ma con probabili influenze cinesi ed indiane.
Terne pitagoriche primitive che, in linguaggio moderno, sarebbero espresse mediante le seguenti formule:
a = 2μν
b = μ 2 − ν 2
c = μ 2 + ν 2
Utilizzando valori di μ e ν primi tra loro e di parità opposta, si ottengono le seguenti terne pitagoriche primitive, con tutti i valori di a, b e c fino a 100 e in ordine di ipotenusa crescente:
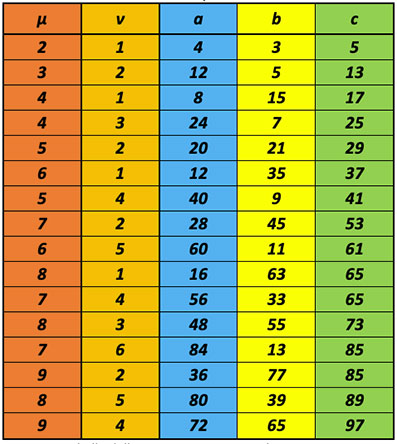
Da ogni terna pitagorica primitiva è possibile ricavarne infinite altre, moltiplicando tutti e 3 i numeri per uno stesso numero λ, così da poter esprimere ogni possibile terna (primitiva o derivata) con le seguenti formule generalizzate:
a = 2λμν
b = λ(μ 2 − ν 2)
c = λ(μ 2 + ν 2)
Per esempio, a partire dalla più piccola terna (3, 4, 5), moltiplicando ogni termine per λ = 2, si ottiene la terna derivata (6, 8, 10) per cui è rimane pure valido 62 + 82 = 102 cioè 36 + 64 = 100 e così via, riuscendo in tal modo ad esprimere ogni possibile terna.[8]
In realtà, Pitagora immaginava i numeri come figure, una rappresentazione di enorme efficacia visiva, che è estremamente attraente ancora oggi ma che sarà oggetto d’attenzione della prossima parte.
Vaffa il gurū, va… e due (δύο)

[1]I «25 lettori» si uniscano a «Carneade» nella richiesta a Manzoni di un risarcimento postumo per l’incomodo.
[2]Claudi Alsina, El club de la Hipotenusa, Editorial Ariel (Barcelona, 2008)
[3]Daniel F. Mansfield, N.J. Wildberge, «Plimpton 322 is Babylonian exact sexagesimal trigonometry» (Historia Mathematica, 2017).
[4]Fino a poco tempo fa, per popolarità e numero di edizioni a stampa, il manuale di Euclide era superato solo dalla Bibbia; Leonardo da Vinci, grazie a Dan Brown non ha bisogno di presentazioni, al pari di Lewis Carroll, grazie ad Alice, benché non tutti sappiano il vero nome dell’autore, il reverendo Charles Lutwidge Dodgson; quanto al Presidente, si tratta di James Abram Garfield, il 20° degli USA.
[5]Elisha Scott Loomis, «The Pythagorean Theorem», 1927.
[6]Nell’antica Grecia era così definito il «magnifico sacrificio» che, secondo i manifestanti consisteva di cento buoi, mentre la questura pare affermasse che il numero cento fosse riferito al numero dei «piedi» e che, in tutto, gli animali macellati fossero soltanto 25 quadrupedi o 50 bipedi; in ogni caso un’orribile carneficina.
[7]Studioso bizantino che fu Scolarca dell’Accademia di Atene (410–485 EV), autore di un Commento al I libro degli Elementi di Euclide.
[8]Giorgio T. Bagni, A research of Pythegorean triples, Dipartimento Matematica Istituto Guido Castelnuovo
Sotto l’eteronimo di Gyro Gearloose si cela un uomo rustico, a volte ruvido, fervido praticante di un libero pensiero, che sconfina in direzioni ostinatamente contrarie all’opinione comune.
Afflitto fin dalla nascita da una forma inguaribile di pensiero debole, simile all’agnosìa, prova a curarla con l’applicazione assidua di scienze dure.
E’ cultore di matematiche che, non capendo appieno, si limita ad amare da dilettante appassionato, sebbene poco ricambiato.
Si consola perlustrando sentieri poco battuti, per campagne e colline dove, tra le rovine del passato, resistono ancora bene l’ulivo e la vite.


