
Il Covid con le sue problematiche è servito in qualche modo a ricordarci quanto la matematica informi di sé la nostra vita quotidiana.
Prendiamo la faccenda del distanziamento ottimale.
E’ acclarato che il pericolo pandemico non sia finito e che siano necessari comportamenti individuali e misure di sicurezza per contrastare la diffusione del contagio.
Fra le misure a creare più difficoltà alle attività, c’è quella della distanza minima da mantenere fra le persone per evitare assembramenti.

Di qui il problema di quale migliore disposizione per i posti al ristorante, nelle aule scolastiche ecc. Sembrerebbero solo questioni tecniche, legate a semplici calcoli matematici. Ma in Italia, evidentemente, non tutti la pensano così.
La ministra Azzolina, ad esempio, ha orgogliosamente dichiarato che il Ministero ha sviluppato un software per ottimizzare la disposizione dei banchi, mentre la Fipe (federazione italiana pubblici esercizi) cerca di dimostrare con ogni mezzo come ridurre la distanza di sicurezza.
L’on. Meloni bisticcia con la Questura sul numero massimo disponibile per la manifestazione di Piazza del Popolo.
Un affannarsi a ben vedere abbastanza inutile, considerato che la questione di come ottimizzare lo spazio è stato già risolto ben due secoli e mezzo fa, e precisamente nel 1773 dal matematico francese J-L. Lagrange.

La soluzione del problema, conosciuto con il nome di impacchettamento di cerchi di densità massima, è in grado di offrire a ristoratori, dirigenti scolastici, questura e a chiunque altro tutte le possibili disposizioni relative al calcolo della densità massima di persone poste a distanza di un metro.
Le soluzioni sono di due tipi.
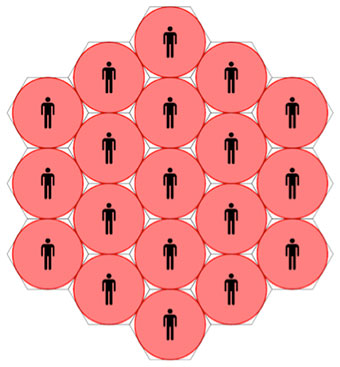
La prima consiste nell’impacchettare il piano con cerchi tangenti di diametro 1 metro, disposti in modo che i tre centri (corrispondenti a tre clienti, tre alunni ecc) di cerchi tangenti formino i vertici di un triangolo equilatero di lato 1 metro.
L’altra soluzione prevede una tassellatura esagonale del piano. Si può tassellare un piano senza lasciare ‘buchi’ solo con tre poligoni regolari: il triangolo equilatero, il quadrato e l’esagono regolare. Quest’ultima è la figura prevista da Lagrange per ottimizzare la copertura del piano.
È la disposizione detta “a nido d’ape” perché ha la forma delle celle negli alveari.
Modelli matematici, ‘previsioni’ della pandemia, “golpe” di Conte.
Uno dei temi caldi della discussione intorno alla pandemia è la validità previsionale offerta dai modelli matematici. La questione rovente all’inizio, affievolita durante il picco, è tornata calda dopo che il prof. Guido Silvestri, capo dipartimento di Patologia all’Università Emory di Atlanta, ha sostenuto che i modelli matematici previsionali sono inadeguati a prevedere l’andamento dell’epidemia e dunque non devono essere usati per prendere decisioni. Una posizione che ha rafforzato il tentativo di esponenti politici di affermare il primato della politica a prescindere dai dati scientifici.
A sostegno della sua tesi Silvestri ricorda che alcuni modelli matematici relativi agli effetti della fase 2 avevano paventato, per l’Italia, 151mila malati in terapia intensiva all’inizio di giugno e invece sono stati appena 286. Può sembrare strano che uno scienziato abbia inteso veramente affermare l’inutilità dei modelli previsionali. Comunque senza entrare nelle reali intenzioni del professore, l’Unione Matematica Italiana ha risposto che quella dei 151 mila in terapia intensiva non era “la” previsione, ma solo una delle 49 possibili evoluzioni della pandemia.
Per l’esattezza, il peggiore scenario possibile.
C’è da dire che il modello matematico dell’epidemia è un sistema complesso, perché piccole variazioni delle condizioni iniziali producono esiti molto diversi. Il fatto di essere di tipo esponenziale fa sì che un minimo cambiamento, un comportamento sbagliato, una decisione politica inadeguata, possono portare a conclusioni a volte profondamente difformi. Vale l’immagine poetica di Lorentz per il quale “un battito d’ali di una farfalla in Brasile può produrre un temporale in Texas”.
Insomma, i modelli non predicono il futuro. Questo dipende piuttosto dalle nostre scelte. I modelli si limitano a disegnare i possibili scenari. Suggerendo implicitamente come evitare quelli peggiori. Che le cose stiano veramente così lo dimostra il diverso andamento del contagio in Italia e nel mondo a seguito delle scelte dei governanti. In Europa, l’uso dei modelli ha evitato un disastro. Non ci sono stati tre milioni di morti solo perché tutto il continente ha seguito l’esempio italiano. La Gran Bretagna ha il numero più alto di morti solo per un piccolo, apparentemente insignificante, ritardo iniziale di chiusura.
È bene ricordare questi dati prima di accusare di golpe il governo italiano che richiede la possibilità d’intervenire d’urgenza in caso di rialzo del contagio.
Matematica calcio muffe e formiche.
Passiamo ad un argomento matematico più lieve. È in libreria il libro di David Sumpter, la matematica del gol. L’autore, un matematico, descrive alcune strategie di gioco paragonandole ai comportamenti degli animali: i difensori del Bayern Monaco aggrediscono l’attaccante avversario con la stessa tecnica di un branco di leonesse a caccia; il tic-toc di passaggi con il quale il Barcellona avanza e prepara l’assalto finale è simile alla rete che produce una muffa per nutrirsi: il calcio totale dell’Olanda di Cruiff imitava l’organizzazione di un esercito di formiche, apparentemente caotico invece soggetto ad una ferrea disciplina, muovendosi come un unico soggetto.

Al termine della lettura sorge spontanea una domanda: è l’allenatore che “vede” questi comportamenti negli animali o questi esistono a prescindere dall’allenatore che non fa altro che imitarli? Domanda antica della filosofia alla quale neppure Kant è riuscito a dare una risposta definitiva.

Quel che è certo è che le scelte degli allenatori poggiano su basi scientifiche. Ormai ogni club ha un suo database che registra i comportamenti dei singoli e delle squadre avversarie. Su questa mole di dati, un esperto analista, spesso un pool, studia poi le tattiche da applicare. Oltre alle conoscenze tecniche, insomma, conta anche la scienza, se è vero che il capo degli analisti del Liverpool, la squadra attualmente più forte al mondo, è un matematico con un dottorato in fisica teorica.
In conclusione, si può affermare che in un gioco di squadra si finisca con il seguire modelli già selezionati dagli animali quando agiscono in gruppo ed essi ottimizzano i loro sforzi applicando il vecchio detto keniano:
“Se vuoi andare veloce corri da solo, se vuoi andare lontano corri insieme agli altri”.
A ben vedere un proverbio e un comportamento squisitamente anti sovranista…

Marcello Ciccarelli, in pensione, attivo solo cerebralmente. Una volta docente e amministratore. Ancora appassionato di matematica e politica.


