Noi lettori d’oggi siamo gente per lo più ben istruita, o almeno assai scolarizzata, molti avendo fatto il liceo e studiato filosofia.
Quindi, abbiamo sentito parecchio parlare di Platone e magari ricordiamo che ebbe Socrate come maestro, poi condannato a morte, pare per empietà – qualcuno di questi tempi, è probabile che lo avrebbe condannato per pedofilìa… ma tralasceremo questi aspetti, non vorrei che pensaste che sono prevenuto.
Beh, fatta questa premessa, vi ricorderete forse anche che Socrate era ostile ai sofisti e che tale avversione trasmise pure al suo allievo, che scrisse molti dialoghi contro di loro; dei trentaquattro dialoghi attribuitigli con certezza dalla critica, almeno sei sono intitolati e/o rivolti ad un qualche sofista e nessuno potrebbe negare che il suo pensiero, in qualche modo, sia una sorte di polemica ininterrotta contro il sofismo, dai «dialoghi aporetici» giovanili fino ai «dialoghi dialettici» della vecchiaia, tanto da intitolare uno degli ultimi proprio al «Sofista» (Σοφιστής), ivi equiparato ad un parricida. Un paio di questi dialoghi («Ippia maggiore» e «Ippia minore») erano contro il più famoso e brillante sofista attivo in Atene, un tal Ippia di Elide.

Vi confesso che, da studente, parteggiavo sfacciatamente per Ippia, tanto che la mia insegnante di filosofia arrivò ad ammonirmi di fare attenzione, nelle mie prese di posizione, altrimenti avrei rischiato di diventare surrettizio quanto il peggior sofista.
Ammonimento che produsse l’effetto contrario, rafforzandomi nella mia direzione ostinata e contraria. Ed ora spero di riuscire a spiegarvi il perché… e non c’entrano niente i pregiudizi contro la maieutica, nemmeno quella praticata in privato da Socrate con i suoi giovani allievi, almeno stando ad alcune dicerie.

Prima di leggere il seguito del pezzo però è utile che vediate un po’ di volte l’animazione seguente, e non esitate a rivederla più volte con attenzione e fissandone nella memoria il movimento e i punti che la caratterizzano, sia la curva (DF), che il quarto di circonferenza (DB), che il quadrato [ABCD], che le contiene entrambe. Si tratta di una «curva meccanica», prodotta dal movimento congiunto ed uniforme dei lati DC (tralazione verso il basso) ed AD (rotazione in senso orario), ed è nota agli specialisti come curva di Ippia di Elide, sì avete inteso bene, proprio il nostro sofista di cui sopra; ammiratela bene:
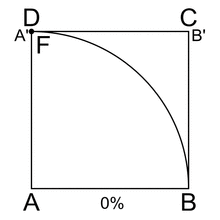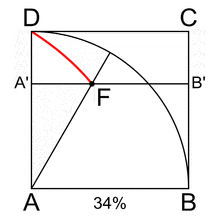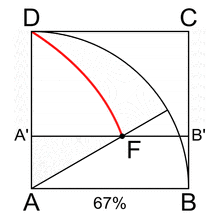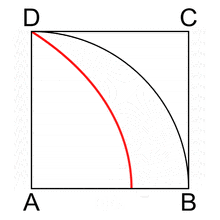
A parte la circonferenza e la retta, si tratta della più antica curva di cui si abbia notizia, nota anche come «trisettrice di Ippia», dal nome del pensatore greco, nativo di Elide, che per primo la descrisse ed usò.
Pare che l’avesse inizialmente definita per fornire una risoluzione al problema della «trisezione dell’angolo», uno dei tre problemi classici della matematica ellenica e che poi, un altro pensatore successivo, Dinostrato, ne abbia scoperto l’utilità pure per la risoluzione dell’altro problema classico, quello della «quadratura del cerchio».
Per cui, in qualche manuale, è chiamata «quadratrice di Dinostrato» ma si tratta sempre della stessa curva – costruita o scoperta che pensar si preferisca – proprio dal nostro Ippia di Elide.
Per inciso, l’Elide è quella regione dell’antico Poliponneso in cui si trovava Olimpia, l’antica città con l’annesso santuario panellenico che diede origine ai giochi olimpici.
Da giovane liceale, vi andai insieme a mio cugino, nel primo memorabile viaggio della mia vita, alla ricerca delle nostre radici… ma questa è una storia diversa, che ci porterebbe da un’altra parte.
Tornando invece a quanto mi sono prefisso: voglio provare a descrivervi come si usa tale curva per quadrare un cerchio e tentare poi alcune considerazioni provvisorie.
Ma come, dirà qualcuno, la quadratura del cerchio? Ma se ci hanno ripetuto ad oltranza che non è possibile quadrare il cerchio? Anzi, tale espressione è diventata un modo di dire proverbiale, a significare il tentare un’impresa impossibile, l’affannarsi su un problema talmente arduo che è illusorio sperar di risolverlo.
Come il combattere contro i mulini a vento…

Alt, al tempo; è vero che è impossibile risolvere il problema ma soltanto se ci si limitasse a volerlo fare usando solo DUE strumenti: il «compasso collassabile» e la «riga non graduata».
Cioè, come fare a pugni con le mani legate dietro la schiena!?!
E a chi poteva venire in mente di fare una cosa del genere, così insensata? A Platone!
E noi posteri a seguirlo pedissequi per quasi duemila anni. Bah…
Ma non divago oltre; torno al punto di partenza, mostrandovi come si quadra il cerchio con la curva di Ippia.
E, per farlo, useremo proprio il punto mobile terminale F della curva (DF), quando tale punto giace sulla base del quadrato, al termine del suo moto.
Il lettore allergico alla matematica non si spaventi, quando incontrerà espressioni che somigliano a formule, del tipo di (DB) : AB = AB : AF, si tratta semplicemente di una «proporzione» tra alcune grandezze, che sono contrassegnate dalle lettere poste ai loro termini.
Un’espressione del genere sta semplicemente a significare che l’arco di circonferenza di misura (DB) «sta» al segmento di misura AB «come» il segmento di misura AB «sta» al segmento di misura AF; intendendo «sta» con il significato di «è in rapporto» ovvero «diviso». Niente di più e niente di meno, è soltanto un modo più agevole e sintetico di esprimerlo e quando, come in questo caso, il secondo ed il terzo termine sono uguali, cioè sono la stessa grandezza, che «sta» nella stessa proporzione tanto con il primo termine (nel membro di sinistra), quanto con il quarto termine (nel membro di destra), allora si dirà che tale termine è «medio proporzionale» tra gli altri due.
E c’è inoltre da sapere che, nelle proporzioni, il prodotto dei termini estremi è uguale al prodotto dei termini medi.
Facciamo un esempio banale:
8 : 4 = 4 : 2
una proporzione valida, poiché entrambi i suoi membri, quello di sinistra e quello di destra rispetto al segno di uguale, sono due rapporti che valgono 2, il che ovviamente conferma la summenzionata regola e cioè
8 * 2 = 4 * 4
come è immediato verificare. Pur sembrando banale ciò permette, ogni qual volta siano noti «tre» dei «quattro» termini della proporzione, di determinarne pure il «quarto», senza alcun bisogno di doverlo effettivamente misurare. Ad esempio, se nella prima proporzione non avessimo conosciuto il quarto termine (2) ma fosse stato incognito (x)
8 : 4 = 4 : x → 8 * x = 4 * 4 → x = 16/8 = 2
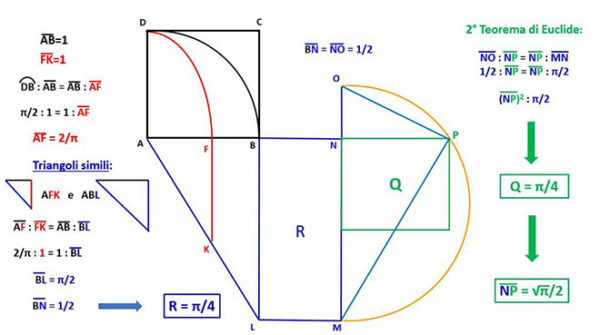
In tutta l’esposizione che seguirà si faccia sempre riferimento alla figura sottostante, che riporta a latere pure i calcoli principali:
Gli studiosi ritengono che Ippia abbia determinato la misura del segmento AF, supponendo che il lato del quadrato AB sia «medio proporzionale» tra l’arco del quarto di circonferenza (DB) ed il segmento AF, cioè
(DB) : AB = AB : AF
Si tenga inoltre presente: (i) che il lato del quadrato è supposto unitario per comodità (AB=1); (ii) che il rapporto tra qualsiasi circonferenza ed il suo diametro è costante e pari a π; (iii) che il quarto della circonferenza, quella contenuta nel nostro quadrante e che ci interessa (DB), è pari a π/2 e che la sua area, compresa tra la curva ed i lati AB ed AD del quadrato, misura π/4, essendo un quarto del cerchio di raggio unitario; tutto ciò considerato, allora la precedente proporzione equivale a
(π/2) : 1 = 1 : AF
da cui, essendo in ogni proporzione il prodotto degli estremi uguale al prodotto dei medi, ricaviamo che
(π/2) * (AF) = 1 → AF = 2/π

A partire da qui, si costruisca un segmento di misura 1, equivalente quindi al lato del quadrato (AB=FK=1), tracciandolo perpendicolarmente al lato AB del quadrato, a partire dal suo punto F individuato dalla curva di Ippia e sia K il suo estremo inferiore.
Dal vertice A, si tracci adesso un segmento passante per il punto estremo K suddetto, fino ad intersecare il prolungamento inferiore del lato BC del quadrato e sia L tale punto d’intersezione.
Siccome per costruzione sono simili il triangolo rettangolo ABL e quello AFK posto al suo interno, i loro lati omologhi staranno nella proporzione seguente:
AF : FK = AB : BL
cioè
2/π : 1 = 1 : BL → BL = π/2
In tal modo, abbiamo appena costruito un segmento di misura π/2 uguale al quarto di circonferenza (DB), cioè abbiamo rettificato una curva. Siccome quell’area è un quarto del cerchio unitario di misura π/4, come detto sopra, allora non ci resta adesso che costruire un rettangolo di lato lungo BL=π/2 e lato corto BN=1/2, per avere il rettangolo R, la cui area misura π/4 proprio come quella del quarto di cerchio (DBO).
Quindi, applicando il 2º teorema di Euclide sui triangoli rettangoli, quello secondo cui l’altezza costruita sopra all’ipotenusa è «media proporzionale» tra le proiezioni dei due cateti, possiamo stabilire la seguente proporzione:
NO : NP = NP : MN
nella quale, sostituendo i termini noti
1/2 : NP = NP : π/2 → NP2 = π/4
Pertanto abbiamo infine ottenuto il quadrato di area π/4, il cui lato misura precisamente √π/2.
Quod erat demonstrandum!

In realtà, quella che avete appena letto è una «ricostruzione» e non una vera e propria «dimostrazione», almeno secondo i canoni moderni; spero comunque sia stata utile a capire lo spirito di un’impresa «sofista».
In conclusione, vorrei tornare però ai sofisti ed alla «nomea» che li ha accompagnati nei secoli.
Platone nei suoi dialoghi li descrisse in modo assai dispregiativo e, sulla falsariga del suo giudizio negativo, pure il suo allievo Aristotele (Ipse dixit…) si unì al coro tanto che, nel linguaggio comune, il termine si caricò così di un significato negativo, per cui «sofisticato» è divenuto sinonimo di artificioso o falso.
A ben riflettere sul motivo per cui essi furono aspramente criticati da Platone e Aristotele, si scopre però che ai sofisti era rimproverato di farsi pagare per i propri insegnamenti: «prostituti della cultura» fu detto.
Oh cribbio! pur non essendo insegnante, permettetemi d’indignarmi contro questo pregiudizio aristocratico.
Hai voglia a contestualizzare… ma questa è più difficile da digerire di quell’altra costumanza! Sì, d’accordo, la forma più comune di relazione sessuale tra i maschi dell’epoca era la «paiderastia» (παιδεραστία), una forma di amore nei confronti dei ragazzi, in genere una relazione intrapresa tra un maschio più anziano ed un giovane adolescente, che veniva considerato «ragazzo» fino a che non gli cresceva la prima barba.

Beh, vi assicuro che sono totalmente laico rispetto ad ogni differenza di genere, e privo di pregiudizi ma voglio non di meno denunciare chiaramente come, a mio avviso, i «minori» non fossero abbastanza tutelati all’epoca.
Voglio denunciare altresì che, nonostante gli splendori dell’età di Pericle, alla mia sensibilità ripugna che all’epoca le donne, gli stranieri (meteci) e gli schiavi non fossero considerati «cittadini»; e ancor più ovviamente mi ripugna che vi fossero uomini ridotti alla condizione di schiavi.
Figlio e nipote di umile gente popolana, d’origine contadina, provo ancora un’avversione naturale, quasi innata, verso chi non deve lavorare per vivere, e chi addirittura trovò scandaloso insegnare dietro compenso.
A me parve da ragazzo che, nel pensiero dei sofisti, si rispecchiassero invece le «esigenze delle alacri classi borghesi, l’arrivismo degli uomini nuovi, l’irriverenza verso le tradizioni sacre ed il beffardo disprezzo del passato».
A me pare pure che «i sofisti furono i primi ad elaborare il concetto occidentale di cultura (παιδεία), intesa non come insieme di conoscenze specialistiche ma come metodo di formazione di un individuo nell’ambito di un popolo o di un contesto sociale».
Per concludere, il sofista mi pare una persona che si guadagnava da vivere vendendo il proprio sapere, quindi un precursore dell’educatore e dell’insegnante professionista dei nostri giorni.
Altro che esecrabile, mi piace pensare che oggi un sofista sarebbe un professionista, un tecnico stimabile.
E Ippia di Elide, con la sua «curva meccanica», così incurante del precetto aristocratico di avvalersi soltanto delle curve più nobili e pure (circonferenza e retta), mi pare il degno campione della sua classe sociale.
Un degno precursore di quel grande genio siracusano che, di lì a poco, avrebbe quadrato molte altre figure e solidi curvilinei e costruito un’altra meravigliosa curva meccanica, la spirale, scrivendo opere di valore inestimabile e assurgendo così ad una fama imperitura: simbolo universale di scienziato.

Sotto l’eteronimo di Gyro Gearloose si cela un uomo rustico, a volte ruvido, fervido praticante di un libero pensiero, che sconfina in direzioni ostinatamente contrarie all’opinione comune.
Afflitto fin dalla nascita da una forma inguaribile di pensiero debole, simile all’agnosìa, prova a curarla con l’applicazione assidua di scienze dure.
E’ cultore di matematiche che, non capendo appieno, si limita ad amare da dilettante appassionato, sebbene poco ricambiato.
Si consola perlustrando sentieri poco battuti, per campagne e colline dove, tra le rovine del passato, resistono ancora bene l’ulivo e la vite.